Comment Trouver L’équation De La Tangente À Une Courbe En Un Point Donné
Découvrez Comment Trouver Une Équation Pour La Droite Tangente À La Courbe Au Point Donné. Maîtrisez Cette Technique Essentielle Pour Vos Études En Mathématiques.
**tangente En Mouvement : Aspect Dynamique**
- La Définition De La Tangente En Mouvement
- Les Applications Pratiques De La Tangente Dynamique
- Comment Calculer La Tangente À Une Courbe
- Les Enjeux De La Tangente En Physique Moderne
- Les Erreurs Courantes Dans L’analyse De Tangentes
- Futur De L’étude Des Fonctions Tangentes Et Dynamiques
La Définition De La Tangente En Mouvement
Lorsqu’on aborde la tangente d’un mouvement, on se retrouve au carrefour de la géométrie et du mouvement, une intersection fascinante qui révèle des principes fondamentaux de la physique et des mathématiques. La tangente, en tant que concept, permet de décrire la direction que prend un objet à un moment précis de son déplacement. En d’autres termes, elle est comme la prescription d’un médecin, indiquant la direction à suivre pour le mouvement à cet instant donné. Imaginons une voiture roulant sur une route sinueuse ; à chaque courbe, la tangente nous fournit l’orientation exacte du véhicule, un peu comme une comp en indiquerait la direction à suivre pour éviter un accident.
Les applications de la tangente en mouvement sont variées et souvent sous-estimées. Dans les domaines de l’ingénierie et de la conception, la capacité à comprendre et à calculer la tangente à un objet mobile permet de créer des machines plus efficaces et sûres. Par exemple, un conducteur de poids lourd doit savoir exactement quand tourner pour éviter une sortie de route, et cette compétence peut être assimilée à “count and pour” pour la conduite, où chaque mouvement est minutieusement prédit pour garantir la sécurité. De plus, dans le monde moderne, les professionnels doivent souvent gérer des données complexes qui requièrent une bonne compréhension de ces concepts dynamiques.
En effet, la tangente est bien plus qu’une simple ligne sur un graphique ; elle représente l’essence même du changement au fil du temps. Dans le contexte actuel, il est impératif d’intégrer cette compréhension dynamique dans l’éducation et la recherche pour ouvrir de nouvelles voies de réflexion. Avec l’émergence de technologies avancées et d’approches innovantes, il est clair que la tangente est une clé essentielle pour unlock les mystères du mouvement, transformant notre compréhension générale des phénomènes physiques.
| Concept | Importance |
|---|---|
| Tangente | Direction du mouvement à un instant donné |
| Applications | Ingénierie, sécurité, dynamique |
| Éducation | Compréhension des principes de mouvement |
Les Applications Pratiques De La Tangente Dynamique
Dans le domaine des sciences et de l’ingénierie, le concept de tangente dynamique joue un rôle crucial. Par exemple, lors de l’analyse de mouvements d’objets, il est essentiel de comprendre la vitesse instantanée. L’élaboration de modèles de mouvement tels que ceux utilisés dans l’automobile implique de trouver une équation pour la reta tangente a curva no ponto dado afin de prédire la trajectoire et optimiser la performance. Ces modeles peuvent ensuite être utilisés pour optimiser la sécurité et l’efficacité, en apportant des solutions innovantes aux défis posés par la physique moderne.
De plus, dans le secteur de la santé, l’analyse dynamique peut également avoir des répercussions significatives. Les pharmaciens, par exemple, utilisent souvent des méthodes de triage pour déterminer le meilleur traitement pour un patient. Cette approche dynamique de la médecine permet de mieux adapter les prescriptions, que ce soit pour des médicaments OTC ou des médicaments sous prescription. Dans des cas plus complexes, il est fréquent de demander des “sig” pour guider les professionnels dans la délivrance de comp-medication spécifiques.
Enfin, dans le cadre de la conception graphique ou de l’architecture, les applications de la tangente dynamique s’étendent également. Les architectes peuvent utiliser ces principes pour élargir les horizons spatiaux de leurs créations. En intégrant des éléments de tangente dans les conceptions, ils peuvent créer des structures plus fluides et fonctionnelles. En comprenant comment les changements dans les angles influent sur l’esthétique et la fonctionnalité, ils se trouvent en mesure de transformer leurs visions en réalités tangibles.

Comment Calculer La Tangente À Une Courbe
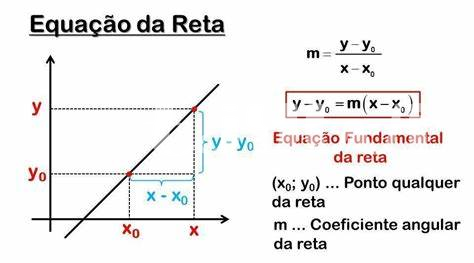
Pour déterminer la tangente à une courbe en un point donné, il est essentiel de comprendre le concept de dérivée. La dérivée d’une fonction à un point précis représente la pente de la tangente à la courbe en ce point. En pratique, si l’on dispose d’une fonction f(x), alors la dérivée f'(x) évaluée au point x0 nous permet d’obtenir la pente recherchée. Après avoir trouvé cette pente, on peut utiliser la forme point-pente de l’équation d’une droite pour établir une équation pour la reta tangente a curva no ponto dado. Ce processus s’applique non seulement en mathématiques, mais il a également des applications pratiques en physique et en ingénierie.
Par exemple, imaginez que vous soyez à une Pharm Party, où certains participants échangent des informations sur la composition des médicaments. Vous pourriez dire que, tout comme les prescriptions peuvent contenir des informations détaillées que l’on doit suivre attentivement, le calcul de la tangente nécessite également une attention minutieuse. Lorsque vous êtes face à la courbe, il est crucial de se rappeler que chaque élément, semblable à un ‘elixir’ dans le domaine pharmaceutique, peut avoir un effet significatif sur le résultat final. Ce lien entre théories mathématiques et applications pratiques démontre comment le calcul de la tangente est non seulement un exercice académique, mais aussi une compétence indispensable dans divers domaines professionnels.

Les Enjeux De La Tangente En Physique Moderne
Dans le cadre de la physique moderne, la tangente joue un rôle central dans notre compréhension des phénomènes dynamiques. Elle permet, par exemple, de décrire comment un objet en mouvement interagit avec les forces qui s’exercent sur lui. En trouvant uma équação para a reta tangente a courbe au point donné, on peut modéliser précisément la dynamique des systèmes en mouvement, qu’il s’agisse d’un projectile ou d’un corps en rotation. Cette approche mathématique est essentielle pour les scientifiques et les ingénieurs, car elle transforme des concepts abstraits en applications concrètes.
L’un des principaux enjeux de la tangente réside dans la capacité à prévoir le comportement futur d’un système. Par exemple, lorsque l’on analyse le mouvement des planètes, comprendre la trajectoire tangentielle permet de prédire leurs positions dans le futur. Les modèles basés sur ces principes servent à l’élaboration de nouvelles technologies, depuis les satellites jusqu’aux systèmes de navigation, où la précision est absolument cruciale.
Par ailleurs, dans le domaine de la mécanique quantique, la tangente revêt une signification plus complexe. Elle peut représenter non seulement la direction du mouvement, mais aussi des aspects probabilistes liés aux comportements d’ondes. Cela montre que la compréhension de ces concepts peut avoir des répercussions sur des domaines variés, allant même à des implications philosophiques sur la nature de la réalité.
Enfin, les erreurs dans l’analyse des tangentes, que ce soit en négligeant des forces ou en simplifiant à outrance des équations, peuvent conduire à des malentendus sérieux dans notre interprétation des phénomènes physiques. Les enseignements tirés de ces erreurs rappellent l’importance d’une rigueur mathématique, un peu comme dans un “prescription” où la moindre confusion peut avoir des conséquences. La consolidation de nos connaissances sur ces dynamiques est donc non seulement une nécessité académique, mais également une obligation éthique pour garantir la sécurité et l’efficacité des innovations technologiques.

Les Erreurs Courantes Dans L’analyse De Tangentes
L’analyse des tangentes est un élément central dans le domaine des mathématiques, mais elle n’est pas à l’abri des erreurs. Une des erreurs fréquentes est l’évaluation incorrecte de la pente de la tangente au niveau d’un point spécifique. Dans beaucoup de cas, les étudiants pensent qu’il suffit de choisir un point aléatoire sur la courbe et de calculer la dérivée en ce point pour obtenir une équation précise pour la droite tangente. Cependant, cela peut mener à des résultats erronés et à une mauvaise compréhension du concept dynamique.
De plus, bien que la notion de calculer la tangente à une courbe semble simple, plusieurs facteurs peuvent complicer le processus. Par exemple, la négligence des points de discontinuité ou des changements brusques dans la direction de la courbe pourrait fausser les résultats. Les étudiants peuvent commettre l’erreur de supposer que la courbe est lisse sans prendre en compte ces éléments essentiels, ce qui entraîne souvent une interprétation biaisée des données et des graphiques associés.
Une autre difficulté se manifeste lors de la manipulation des équations. Il est fréquent de rencontrer des confusions autour des étapes de simplification, particulièrement lorsqu’il s’agit d’appliquer des règles de dérivation. Par exemple, en se précipitant pour obtenir une équation, un étudiant peut ignorer les règles précises et conclure sur une expression qui n’est pas valide. Cette précipitation peut parfois être comparée à une “pharm party” où les participants prennent des décisions rapides sans réfléchir aux conséquences, ce qui est dangereux dans un contexte académique.
Enfin, il ne faut pas oublier l’importance du contexte dans lequel nous manipulons les tangentes. Comprendre l’environnement de la fonction est tout aussi important que les calculs eux-mêmes. Les petites erreurs, comme un signe mal placé, peuvent totalement modifier une pente et conduire à une mauvaise interprétation des résultats. Cela met en lumière la neccessary nécessité d’une approche rigoureuse et d’une vérification minutieuse. Voici un aperçu des principaux points d’erreur dans l’analyse des tangentes :
| Type d’erreur | Description |
|---|---|
| Pente incorrecte | Évaluation erronée de la pente au point donné. |
| Discontinuités ignorées | Ne pas tenir compte des points de discontinuité dans la courbe. |
| Manipulations inexactes | Erreur lors de l’application des règles de dérivation. |
| Contexte négligé | Ignorer l’environnement de la fonction lors de l’analyse. |
Futur De L’étude Des Fonctions Tangentes Et Dynamiques
L’étude des fonctions tangentes et dynamiques est sur le point de révolutionner plusieurs domaines, allant des mathématiques pures aux sciences appliquées. Avec l’avènement des nouvelles technologies, comme l’intelligence artificielle et les systèmes d’analyse avancée, les outils permettant d’explorer ces concepts deviennent plus accessibles. Par exemple, dans un environnement où les calculs en temps réel sont critiques, la capacité de déterminer la tangente d’une courbe âme à un instant donné peut aider à des applications variées, telles que la modélisation de flux en pharmacologie. Dans ce contexte, le “Drive-Thru” de la recherche scientifique permet de “Count and Pour” les découvertes et d’optimiser les prescriptions des traitements.
Par ailleurs, les défis posés par le “Pharmageddon” du dosage et de l’administration des médicaments nécessitent une meilleure compréhension des fonctions dynamiques. Les chercheurs s’attachent à comprendre comment la dynamique des systèmes influence le comportement des médicaments, et cela pourrait entraîner une nouvelle ère dans le développement de traitements plus ciblés. Ce qui était autrefois considéré comme une approche théorique pourrait devenir une pratique courante, notamment grâce à des solutions comme les “Elixirs” pharmaceutiques, qui combinent plusieurs fonctions dynamiques pour optimiser l’efficacité des traitements.
Enfin, l’essor des données massives et de l’apprentissage automatique semble prometteur pour l’avenir de cette discipline. À mesure que les systèmes sont capables d’analyser de vastes quantités d’informations en un temps récord, la vision des fonctions tangentes appliquées pourrait s’étendre au-delà des mathématiques, en influençant la manière dont nous concevons les traitements de santé. Ainsi, le futur de cette recherche offre des perspectives excitantes, rendant des concepts autrefois abstraits, tels que les “Happy Pills” d’une approche personnalisée, maintenant visibles et mesurables grâce à une compréhension approfondie des dynamiques au sein des systèmes biologiques.