Découvrez Comment Trouver Les Équations De La Droite Tangente Et Normale
Apprenez À Trouver Facilement Les Équations Pour La Droite Tangente Et La Droite Normale Grâce À Des Concepts De Dérivées. Éclairez Vos Compétences En Mathématiques !
**dérivées Et Tangentes : Un Lien Essentiel**
- La Dérivée : Une Notion Fondamentale En Calcul
- Comprendre La Pente Grâce À La Tangente
- Applications Pratiques Des Dérivées Dans La Vie Réelle
- Dérivées Et Tangentes : Concepts Interconnectés
- Illustration Graphique : Dérivée Et Droite Tangente
- Importance Des Dérivées Et Tangentes En Mathématiques
La Dérivée : Une Notion Fondamentale En Calcul
La dérivée, concept fondamental en calcul, sert à mesurer comment une fonction change. En d’autres termes, elle représente le taux de variation d’une fonction par rapport à une variable. Sur cette base, on peut situer l’importance des dérivées dans de nombreux domaines, y compris la physique et l’économie. Imaginez que vous êtes un pharmacien qui doit ajuster rapidement la dose d’un médicament pour un patient – c’est ici que la notion de dérivée devient cruciale, car elle permet de quantifier cette modification de manière précise. Les dérivées nous permettent également de mieux comprendre la relation entre des médicaments, comme un élixir qui pourrait être enrichi ou affaibli selon les besoins spécifiques du patient.
Dans l’apprentissage des mathématiques, aborder les dérivées ouvre la porte à une multitude d’applications pratiques. En effet, elles nous permettent d’optimiser des processus, que ce soit en pharmacie ou dans d’autres secteurs similaires. Par exemple, l’analyse des dérivées est essentielle pour déterminer le meilleur moment pour administrer une médication en fonction des pics d’efficacité ou des effets secondaires. C’est le même principe que pour la gestion des stocks au sein d’une pharmacie, où chaque décision doit être prise en fonction des données en temps réel, un peu comme le processus de “count and pour” lors du remplissage des prescriptions.
À travers des applications variées, la dérivée se connecte à de nombreux problèmes réels. En pharmacie, cette notion aide à croire que derrière chaque prescription (Rx), chaque “sig” ou directive, se cache une analyse mathématique rendant tout possible avec précision et efficacité. En résumé, la compréhension des dérivées est non seulement essentielle pour les mathématiques, mais elle est également une compétence indispensable à travers plusieurs champs d’expertise, permettant de combiner théorie et pratique de manière harmonieuse.
| Concept | Application |
|---|---|
| Dérivée | Mesure du taux de variation |
| Taux de variation | Analyse des effets des médicaments |
| Optimisation | Gestion efficace des stocks |
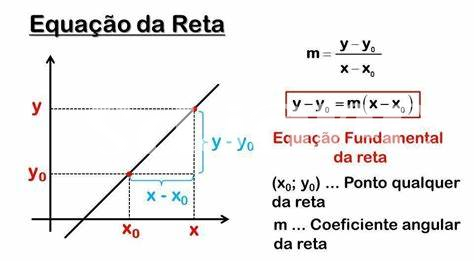
Comprendre La Pente Grâce À La Tangente
Dans le monde des mathématiques, la pente d’une courbe est bien plus qu’un simple chiffre ; elle représente la relation dynamique entre deux points sur cette courbe. L’idée de la tangente provient de la nécessité d’évaluer cette pente à un moment précis, soit à un point donné. En fait, la tangente est, au fond, l’outil qui nous permet de décrypter ce changement. Imaginez-vous à la fenêtre d’une pharmacie, observant le monde autour de vous. Chaque mouvement a une direction, une accélération, tout comme la courbe d’une fonction dans un graphique. Quand on trace la droite tangente, on peut observer une approximation parfaite de la pente, exactement comme un prescripteur évalue un médicament spécifique pour répondre à un besoin immédiat d’un patient.
En analysant ces notions, on peut dire que lorsqu’on rencontre equações para a reta tangente e para a reta normal, on entre dans un univers où chaque détail compte. Grâce à la tangente, nous pouvons non seulement calculer la pente à un point, mais également déterminer comment elle change autour de ce point. C’est un peu comme administrer des “happy pills” à un patient ; la bonne mesure peut apporter un réconfort immédiat. En mathématiques comme en médecine, comprendre les nuances de la pente et de la tangente permet d’atteindre un équilibre, essentiel pour des résultats significatifs.
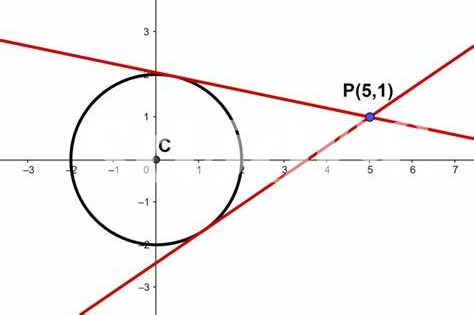
Applications Pratiques Des Dérivées Dans La Vie Réelle
Les dérivées jouent un rôle essentiel dans de nombreux domaines, y compris la finance et la physique. Par exemple, dans le monde de l’économie, les entreprises utilisent les dérivées pour analyser et optimiser leurs profits. En modélisant les coûts et les revenus, elles peuvent trouver la dérivée de la fonction de profit pour déterminer le moment où leur profit est maximal, ce qui est crucial pour une bonne stratégie commerciale.
En physique, les dérivées permettent de décrire des mouvements. Lorsqu’un objet se déplace, la dérivée de sa position par rapport au temps nous donne sa vitesse. Ainsi, si nous voulons enseigner à un étudiant comment une voiture accélère ou ralentit, on lui demandera de encontre équações para a reta tangente e para a reta normal pour illustrer le changement de vitesse à un instant donné. Cette approche rend l’apprentissage plus concret et pertinent.
Dans le domaine de la biologie, les dérivées aident à comprendre les taux de croissance des populations. Les biologistes utilisent des modèles mathématiques pour prédire comment une espèce évolue au fil du temps, et encore une fois, la dérivée fournit des informations sur la rapidité de ce changement. De cette manière, ils peuvent prendre des décisions éclairées concernant la conservation des espèces.
Enfin, l’industrie pharmaceutique utilise les dérivées pour optimiser la délivrance de médicaments. En ajustant les dosages et les temps d’administration, il est crucial de comprendre comment la concentration d’un médicament dans le sang varie au fil du temps. Les professionnels de santé se basent sur ces dérivées pour créer des traitements efficaces et adaptés aux besoins des patients.
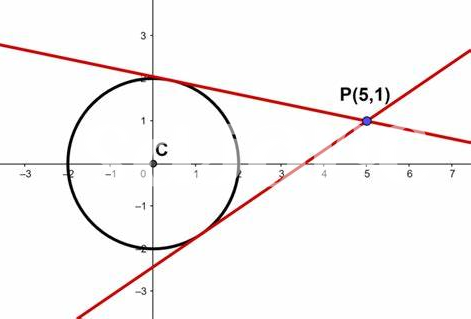
Dérivées Et Tangentes : Concepts Interconnectés
Les dérivées et les tangentes sont intimement liées, formant un duo essentiel pour comprendre le comportement des fonctions. En effet, la dérivée d’une fonction en un point donné représente la pente de la droite tangente à la courbe en ce même point. Cette pente nous donne une idée précise de la variation de la fonction à cet instant précis. Lorsqu’on aborde ces concepts, on peut facilement rencontrer des équations pour la droite tangente et pour la droite normale, qui sont toutes deux fondamentales pour l’analyse des graphiques.
La droite tangente, par définition, touche la courbe d’une fonction en un point sans la couper, illustrant ainsi la direction dans laquelle la fonction évolue à cet instant-là. De ce fait, il est primordial de comprendre comment ces tangentes peuvent être utilisées pour prévoir le comportement d’une fonction dans les domaines d’application variés, allant de la physique à l’économie. Une simple équation peut donner lieu à une multitude d’interprétations.
Au-delà de la théorie, ces concepts ont des applications pratiques. Par exemple, dans le domaine médical, la capacité de modéliser des variations de dosage de médicaments peut être visualisée à travers les dérivées, ce qui permet d’ajuster un traitement au besoin du patient. Cela ressemble au travail d’un pharmacien qui, après avoir analysé les données, peut recommander un ajustement de la prescription basé sur des observations cliniques.
Enfin, la compréhension des dérivées et des tangentes renforcent notre capacité à appréhender des phénomènes complexes. En manipulant ces concepts, on peut anticiper des résultats et optimiser des processus, ce qui est essentiel pour réussir dans des disciplines telles que l’ingénierie ou l’économie. Chaque équation résolue, chaque pente calculée, nous rapproche d’une maîtrise plus approfondie des outils mathématiques dont nous avons besoin pour naviguer dans notre environnement quotidien.
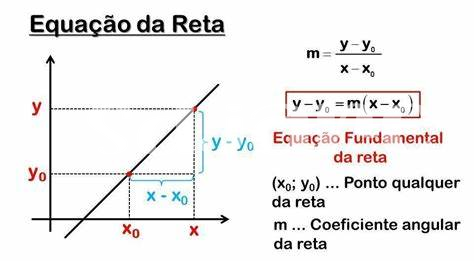
Illustration Graphique : Dérivée Et Droite Tangente
La visualisation de la relation entre la dérivée et la droite tangente est essentielle pour saisir l’idée de la variation d’une fonction. En effet, la droite tangente, qui est la meilleure approximation linéaire d’une courbe à un point donné, est déterminée par la dérivée. Cette dernière donne la pente de cette droite et peut être comprise comme la vitesse de changement de la fonction à ce point. En parles de trouve les équations pour la reta tangente et pour la reta normal, qui sont des outils mathématiques pratiques pour étudier les comportements des fonctions. Il est fascinant de constater à quel point la géométrie et l’analyse se rejoignent pour offrir des solutions pratiques.
Pour illustrer cette connection, un graphique regorgeant de courbes peut démontrer comment la pente d’une fonction varie et comment la tangente s’adapte à celle-ci à des points cruciaux. En assimilant ces concepts visuellement, nous facilitons leur compréhension et leur application efectiva. Par exemple, dans des scénarios courants comme la pharmacie, des graphiques peuvent aider à prédire les effets des medicaments en fonction du temps, en utilisant des modèles basés sur des données de patients. Ainsi, le lien entre dérivée et tangente ne se limite pas à une simple abstraction mathématique, mais touche aussi des domaines comme la santé et le bien-être.
| Concept | Dérivée | Droite Tangente |
|---|---|---|
| Définition | Pente de la fonction | Approximation linéaire à un point |
| Équation | f'(x) | y – f(a) = f'(a)(x – a) |
| Applications | Analyse de la variation | Résolution de problèmes d’optimisation |
Importance Des Dérivées Et Tangentes En Mathématiques
Les dérivées et les tangentes jouent un rôle crucial dans le monde mathématique, devenant presque une prescription pour déchiffrer la complexité des fonctions. En effet, ces concepts permettent de transformer une simple courbe en une riche information sur le comportement d’une fonction à un point donné. Grâce à la dérivée, on peut comprendre la variation instantanée d’une fonction, ce qui est comparable à l’analyse précise d’un médicament avant administration : il est essentiel de connaître son effet immédiat pour anticiper les résultats escomptés.
En médecine, chaque prescription est accompagnée d’indications claires, tout comme la dérivée offre des instructions sur la pente à un point spécifique. Considérer la tangente à une courbe, c’est comme scruter les directions sur un Rx ; cela nous donne une vision immédiate de la tendance, qu’elle soit ascendante ou descendante, nous permettant ainsi de gérer des situations complexes avec précision. Cette connexion entre la variation instantanée et les tangentes s’articule autour de la possibilité d’anticiper les comportements futurs.
Les applications des dérivées et des tangentes s’étendent bien au-delà des frontières de la théorie mathématique. Dans des domaines variés tels que l’économie ou la physique, ces concepts sont utilisés pour modéliser des phénomènes, tout comme dans le domaine pharmaceutique où un pharm tech doit régulièrement évaluer l’âge des médicaments dans le frigo et adapter les traitements. La capacité à prédire les résultats en fonction des fluctuations des données est indéniablement liée à la compréhension des dérivées.
Enfin, il est important de reconnaître que sans une solide maîtrise de ces notions, il serait difficile de naviguer dans un environnement mathématique qui devient de plus en plus complexe. Les dérivées, tout comme les instructions sur un médicament sur le comptoir, apportent un éclairage indispensable qui aide à garder un œil sur les comportements des fonctions, soutenant ainsi tant les étudiants que les professionnels dans leur quête de solutions.